中文标题：基于LPR数据的可拓展高斯混合排队长度估计模型

作者：Chaofeng Tan, Hao Wu,Keshuang Tang, and Chaopeng Tan*

已见刊于：Journal of Advanced Transportation.

http://doi.org/10.1155/2022/5119209

关键词：车道排队长度估计，高斯混合模型，车牌识别数据

排队长度被广泛认为是信号控制路口的关键性能指标。车道排队长度能够反映交通信号的容量，并提供车道间队列分布信息，对交叉口主动交通管控至关重要。近年来，许多研究开始利用车牌识别（LPR）系统的数据来估计排队长度。然而，目前的研究尚未提供可靠的方法，来解决基于可能存在漏检的单一交叉口电子警察（LPR）数据的车道排队长度估计问题。本文旨在通过引入一种基于数据驱动的统计方法，来对基于单截面车牌识别数据的车道排队长度进行估算。

首先，本文通过处理车牌识别数据，获得了每个周期的每辆车地离开时间序列（以绿灯相位开始时间为原点）。然后，本文假设排队车辆和非排队车辆属于时间间隔分布和离开时间分布的两个不同的二维分布，采用了一种概率聚类模型，即高斯混合模型（GMM），基于LPR数据识别车辆的排队状态（排队或非排队），并采用期望最大化算法解出模型中的参数。最后，本文通过二维高斯混合模型识别出每辆记录车辆的排队状态，并根据周期内最后一个排队车辆估计最大排队长度。本文还指出，在通常实际应用中，可以使用在同一时间段的同一工作日的历史LPR数据来校准GMM，并基于实时LPR数据估计基于周期的排队长度。最终获得的流程图如下：

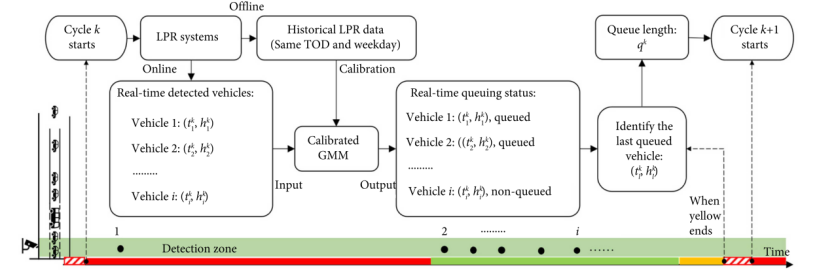
图1 LPR系统的检测过程

本文还指出：尽管研究的主要目标是使用单截面车牌识别（LPR）系统实现排队长度估计，但本研究方法可以通过综合考虑车辆行驶信息，构建一个利用多个横截面（上下游交叉口）LPR数据的三维高斯混合模型。

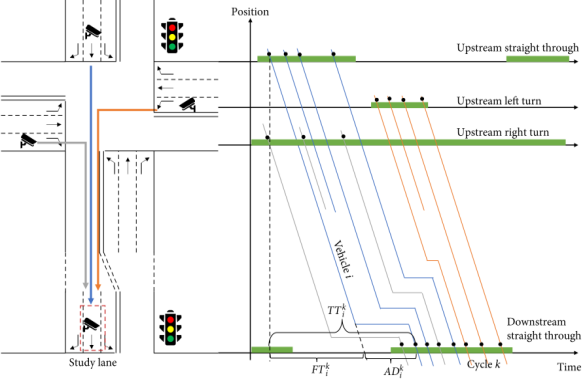
图2 多截面车牌识别（LPR）系统车辆检测示意图

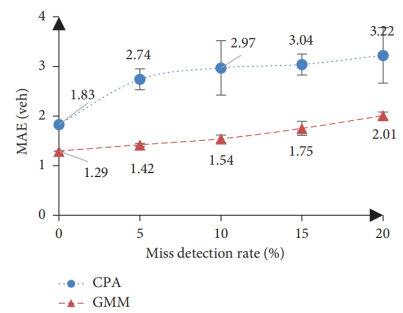
本文分别在基于实证数据和仿真数据的情况下进行了评估。实证评估中，采用了江苏省常州市金陵路-河海路交叉口的实证数据，并复现了现有方法CPA法做为对比，实证结果显示，所提出的GMM方法在不同漏检率下比现有方法具有更高的准确性和稳定性。在两小时的分析周期内，当没有漏检时，GMM方法的平均绝对误差（MAE）仅为1.29辆/周期。即使在20%的漏检率下，GMM方法的MAE也仅为2.01辆/周期。

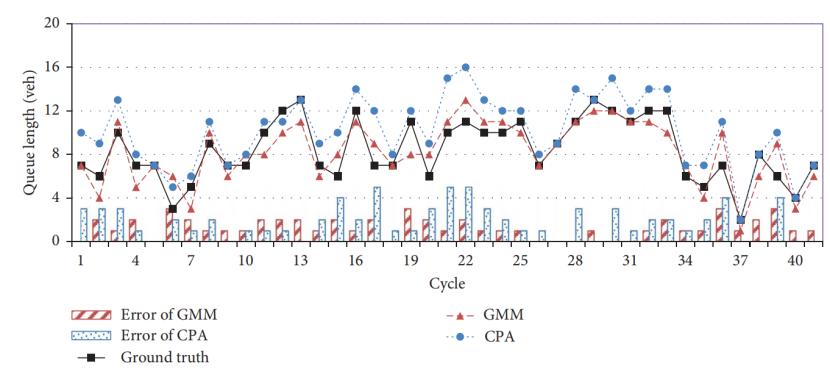
(a) 基于周期估计

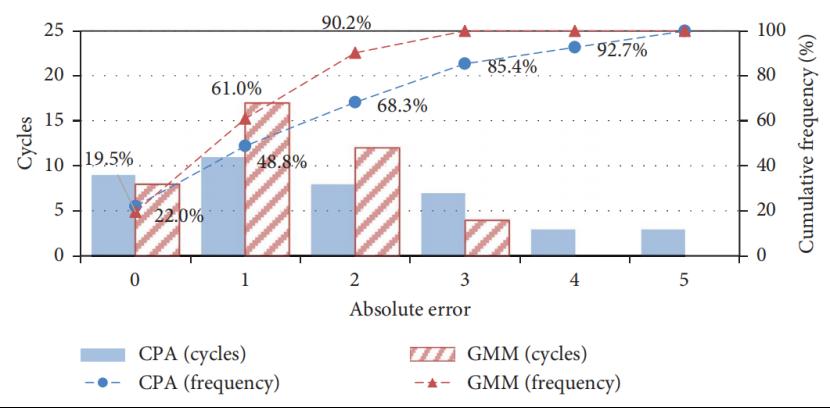
(b) 误差统计

图3车道排队长度的周期估计

图4不同漏检率下的估算结果

在仿真数据评估中，随着d/c值的增加，MAE略有上升，但由于更高d/c值下更长的地面真实队列长度，MAPE有所下降。

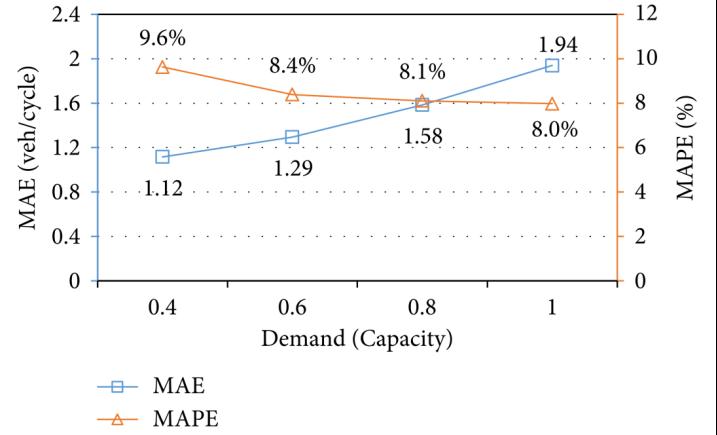
图5 不同d/c水平下的总体估计准确度

此外，研究还在多个横截面LPR数据情境下进行了测试，发现更充分地利用从LPR数据中获得的有效信息，有助于更精准地识别LPR系统检测到的车辆排队状态。

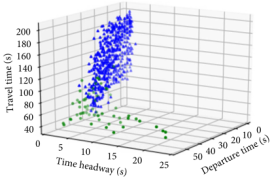
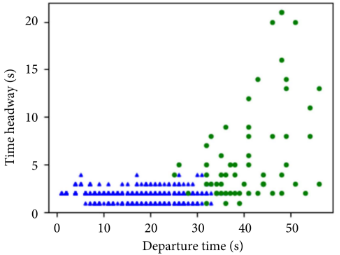
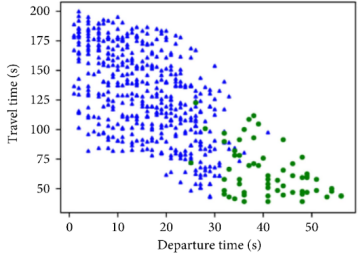
图6 多截面LPR数据下GMM结果

本文的主要贡献在于：（1）提出了一种基于单截面LPR数据的车道队列长度估算方法，可进一步扩展至多截面LPR情景。（2）所提出方法的统计特性使其在LPR数据存在漏检时依然可靠，填补了当前研究的空白。（3）在不同的漏检率下，所提出方法的性能优于现有方法。