作者：Jiarong Yao, Fuliang Li, Keshuang Tang*, Sun Jian.

已见刊于：IEEE Transactions on Intelligent Transportation Systems. Vol. 21, No. 6, pp. 2615-2627, June 2020. DOI: 10.1109/TITS.2019.2921478.

关键词：信号控制交叉口、流量估计、抽样轨迹数据、交通冲击波理论、有界时变泊松过程、M3分布

在城市道路信号控制交叉口，周期级到达流量对交通状态估计和信号控制优化具有重要作用。传统的交通检测主要是通过以线圈为代表的固定检测器获取流量数据从而对实际到达流量进行估计，但是固定检测器的布设范围有限，而且还存在检测失效的问题。随着车辆定位和车联网技术的发展和普及，实时的轨迹数据逐渐应用于城市交通管理。轨迹数据一方面传输频率要小得多，比起定点检测器数据一般为10-60秒的传输频率，能够捕捉到更准确的车流信息；另一方面，轨迹数据的应用空间范围没有限制，更适用于路网层面长期宏观的检测需求，在交通检测和管理系统的应用具有良好前景。

传统流量估计的研究主要是基于定点检测器实现，预测方法包括滤波算法等数理统计方法和基本图、元胞传输模型等模型解析法。基于定点检测器的流量估计方法主要存在设备布设和维护成本高、上传频率低的问题，而且得到的速度、流量等检测指标是基于检测步长的平均值，不能体现交通流的波动性和随机性。随着轨迹数据的出现，使用轨迹数据用于流量估计的研究可以分为两类：一类沿用传统数理统计和解析方法，只是更换了数据源；另一类方法则是根据轨迹数据的特征提出专门定制化的处理和建模思路。其中数理统计方法一般是历史检测数据实现，而且模型参数大多需要实证数据标定；采用滤波算法或者基本图要基于历史数据拟合交通流参数的关系，一般性较差。此外，基于轨迹的方法研究难点还在于如何确保低捕获率场景下的估计精度，因此，建立一个一般性和适用性较强的周期流量估计方法对于轨迹数据的进一步应用推广具有重要的现实意义。

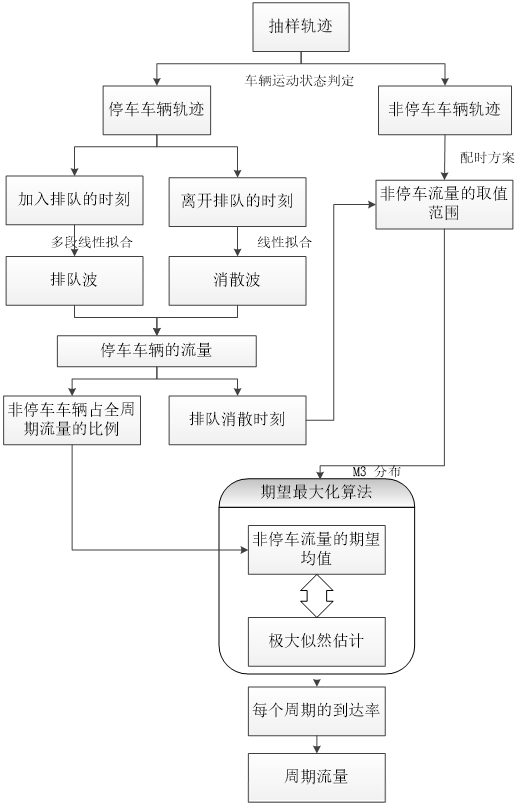
图1 技术流程

图1简要诠释了本方法的技术流程。首先，获取抽样车辆的轨迹点数据，并基于轨迹点的速度判断车辆所处的运动状态，将抽样轨迹分为排队停车的轨迹和非排队直接通过交叉口的轨迹，并针对停车轨迹通过内插法确定车辆加入或离开排队的关键点。对同一周期内所有停车抽样轨迹的关键点，利用多段线性拟合对车辆排队的集结波和消散波进行估计，并计算两个交通波的交点作为排队车辆的流量估计值，如图2所示。针对非排队轨迹，则将非排队车辆的到达过程假设为有限取值的泊松分布，相应地车头时距服从M3分布，根据压缩波计算全部排队车辆以及红灯期间到达车辆消散的时刻，计算该周期的队列比、非排队车辆的车头时距取值范围等参数。由此，本文将全周期的流量估计问题转化为融合了交通波理论重构排队和基于非排队车辆的泊松分布和M3分布的参数估计问题，通过极大似然估计法对全周期的到达率进行估计，并用期望最大法（EM）求解，即可得到每个周期的到达流量。

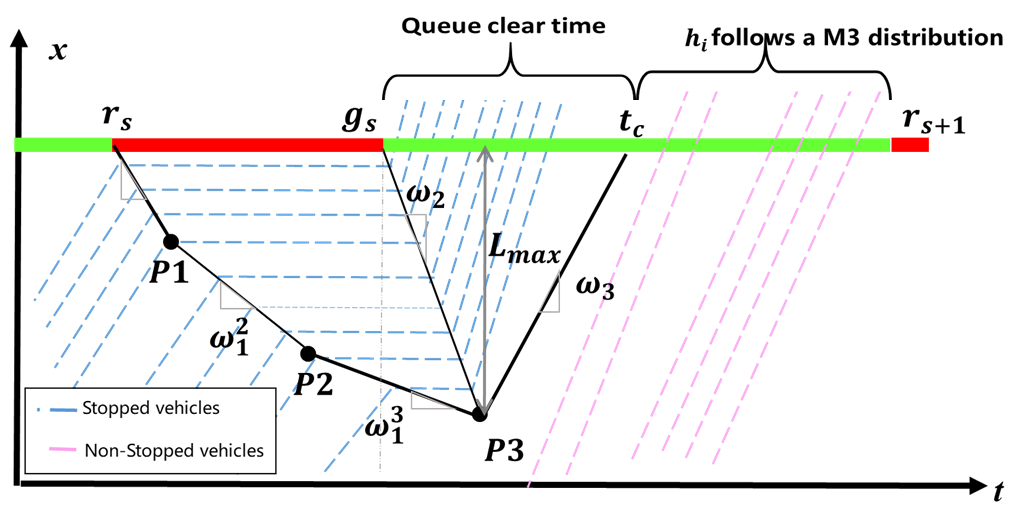
图2 融合方法示意图

本方法通过深圳市皇岗路-福中路交叉口的实证数据进行了验证，在五个小时囊括六个TOD方案的验证时段内，算法在抽样轨迹的平均捕获率为7.6%的条件下，时段流量估计精度达95%以上，周期流量估计精度达80%以上。并且针对实证验证场景建立了对应的仿真模型对饱和度和捕获率进行了敏感性分析。结果标明本方法能够充分挖掘轨迹数据信息，对不同的交通需求场景具有较好的适应性，在低捕获率条件下仍然能得到较高的估计精度，模型可靠性较好。