作者：Yu Mei，Weihua Gu，Edward C.S. Chung，Fuliang Li，Keshuang Tang.

已见刊于：Transportation Research Part C: Emerging Technologies 109 (2019): 233-249, https://doi.org/10.1016/j.trc.2019.10.006

关键词：排队长度估计、浮动车轨迹数据、贝叶斯算法、最大期望算法

交叉口的交通信号交替给予不同方向行驶的车辆通行权，导致各途径车辆队列的重复形成和消散。车辆排队从停止线传播的最大距离，在文献中通常称为最大排队长度，已被普遍用作信号性能的衡量标准，并作为优化信号相序和相位差的关键输入。估计最大排队长度是城市交通管理和控制的一项重要而富有挑战性的任务。

在该方法中，利用每个信号周期所给出的排队长度的上界和下界估计排队长度的分布。从加入排队的探测车辆轨迹数据中得到一个下界，称为停止车辆。利用不符合队列的探测车辆(称为不停止车辆)的数据，给出了一个上界。本估计方法主要包含以下几个步骤：（1）识别停止车辆和非停止车辆；（2）推导后验分布；（3）估计排队长度；（4）更新先验。

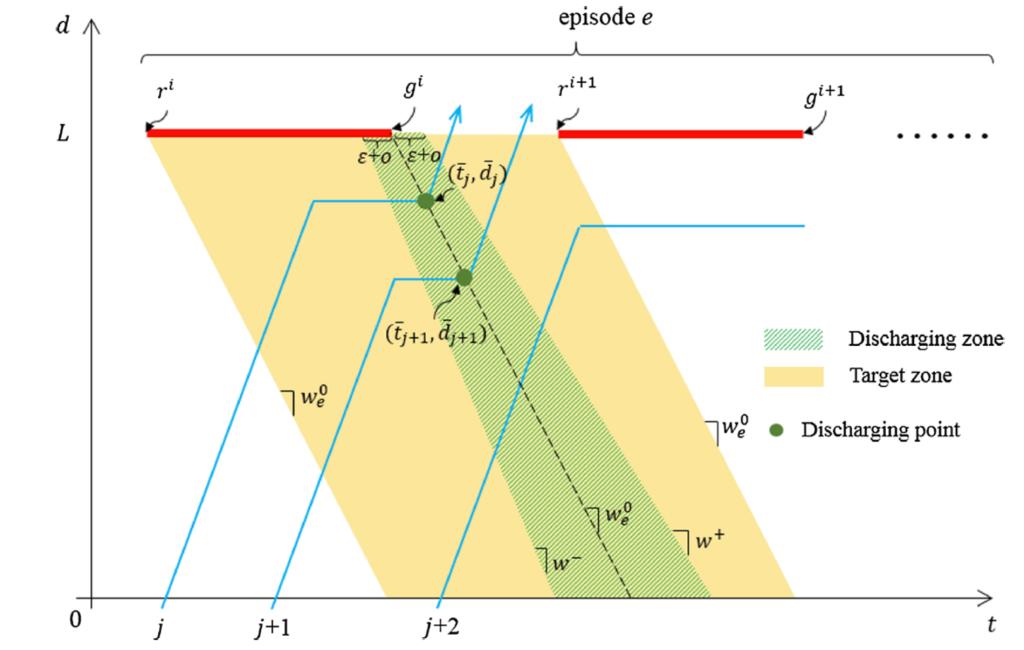
图1 车辆识别空间

对本方法进行仿真测试，对于20%和2%两种典型的渗透率场景进行测试，如下图所示，饱和度设置为70%。图中的蓝线表示探测车的轨迹。虚线表示估计的释放冲击波。冲击波上绿色圆点表示已停车辆的释放点，黑色方块表示释放冲击波与每个周期第一个未停车车辆轨迹的交点。黄色阴影框表示在每个周期中上下边界之间的范围。黑色实线表示估计的排队长度，洋红色虚线表示实际排队长度。

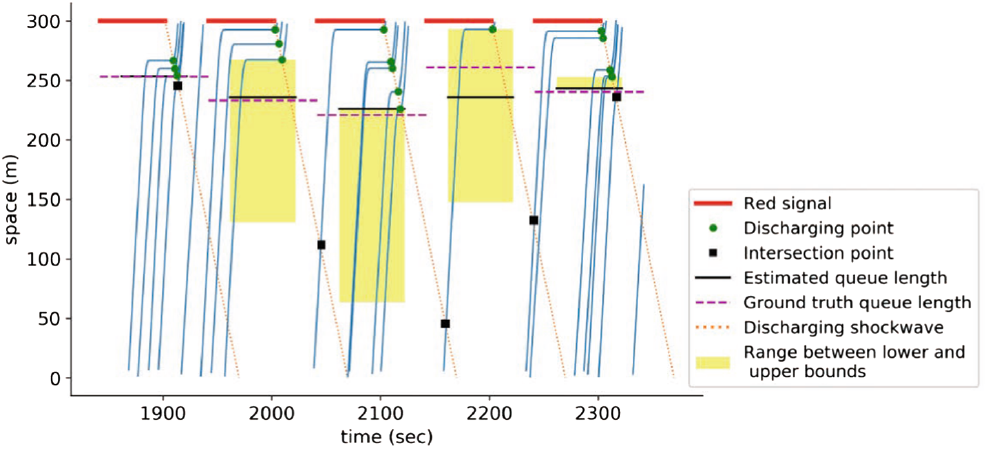
（a）高渗透率（20%）

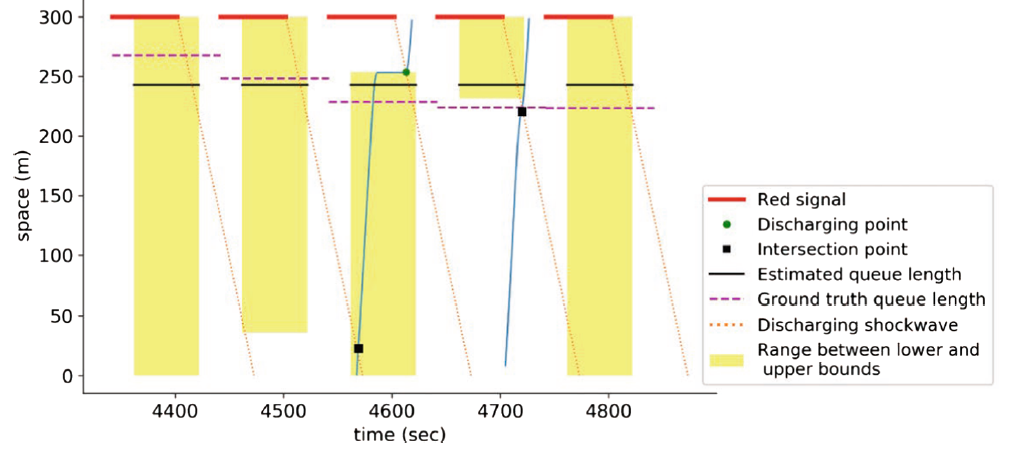
（b）低渗透率（2%）

图2 不同渗透率场景下的测试结果

此外，又将此方法与Ramezani和Geroliminis(2015)以及Li et al.(2017)分别提出的两种方法的估计误差进行比较。这三种方法都不依赖于关于车辆到达过程的假设和已知的渗透率。因此，这三种方法更适合在更动态的交通条件下应用。在Ramezani和Geroliminis中，排队长度是根据周期中最后停止车辆的位置来估计的；也就是说，它们的估计值是此方法中的下界。Li等通过计算释放冲击波和释放形成冲击波的交点来得到估计。两种方法都忽略了未停车的车辆，如果在一个周期中检测到未停车的车辆，则不进行估算。

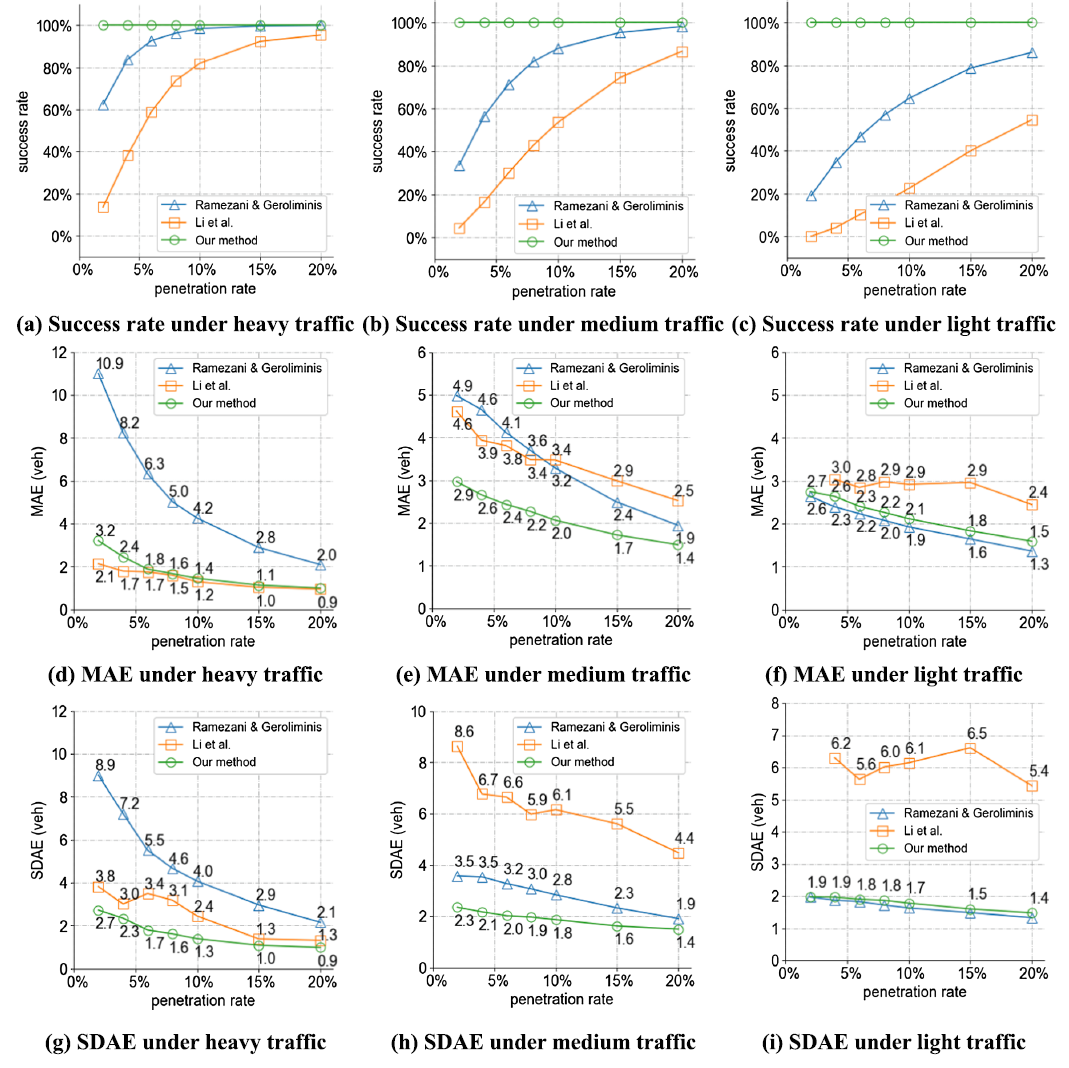
图3 三种方法对比

在大多数情况下，本研究提出的方法的估计显示的MAE只有1~3辆车，优于其余两种方法。同时，当对所有周期进行估计时，无论周期是否包含探测车辆数据，都可以获得较低MAE。相比之下，另外两种方法的成功率都很低，特别是在低渗透率下。此外，该研究所提出的方法提供了更稳健的估计，其表现为在变化交通条件和探测车辆频率下提供持续的低MAE和SDAE。