中文标题:基于抽样轨迹数据的信控交叉口累计流图估计与预测
作者: Chaopeng Tan, Jiarong Yao, Xuegang (Jeff) Ban, Keshuang Tang *.
已见刊于:IEEE Transactions on Intelligent Transportation Systems. 08/11/2021, Early access.
https://doi.org/10.1109/TITS.2021.3102750
关键词:累计流图,信控交叉口,抽样车辆轨迹,排队长度,交通流量,停车延误
尽管目前已有大量的研究致力于基于网联车辆轨迹数据实现交叉口交通状态指标估计,现有研究依然存在以下局限:1)大多数研究的模型仅能实现单个或两个指标的估计。例如,尽管基于交通波理论的排队长度估计方法可以进一步实现停车延误的估计,交通流量和平均延误等指标依然无法获取。2)目前,现有研究都无法完整地描述交叉口所有车辆的到达和离去过程。虽然基于交通波的方法可以重构排队车辆的到达和离去过程,但并未重构非排队车辆。基于概率论的方法则通常需要特定的假设来描述车辆的到达和离去过程,然而这些假设通常过于理想化,与实际不符。3)现有的研究仅仅只能实现交通状态的估计,并未将其与信号配时参数联系起来,因此还需要进一步依赖传统延误或排队模型来实现信号控制优化。
此外,目前在亚洲国家,绝大多数信号控制交叉口依然采用多时段定时的方式运行,例如中国和日本分别有95%和48%的城市道路信号控制交叉口采用固定配时。同时,大规模应用车联网等技术依然需要数十年时间。因此,在这个过渡阶段有必要研发一种高效的方法,基于历史的网联车辆轨迹数据来实现定时信号控制交叉口的运行评价与优化。
为了弥补现有研究的缺陷,本研究面向多时段定时信号控制交叉口,提出一种基于网联车辆轨迹数据的交叉口累计流图估计和预测方法。累计流图(Cumulative Flow Diagram,CFD)是一种描述交叉口所有车辆到达和消散过程的流率时变图(如图1所示),基于累计流图可以实现前述多个交通参数的同时估计,包括流量、排队长度和延误等,从而实现交叉口交通状态的全面评估。此外,与交通波方法仅能描述排队车辆的到达和离去过程相比,累计流图还描绘了非排队车辆的到达(可能的累计过程)和离去过程,使其可以进一步用于交叉口的信号控制优化。
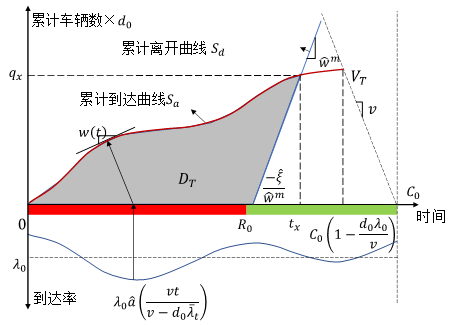
图1 累计流图示意图
方法框架如图2所示。
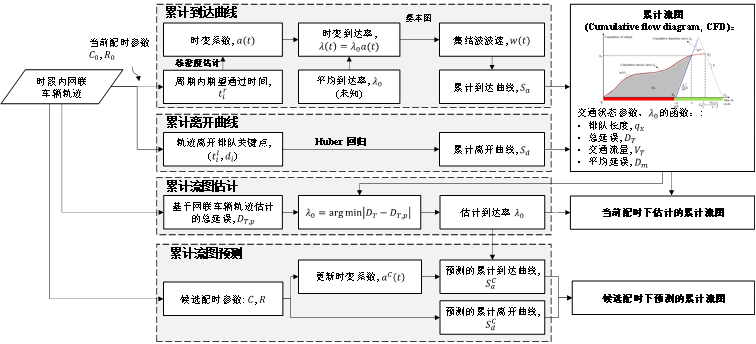
图2 网联车辆轨迹数据驱动的交叉口累计流图演化框架
首先,基于历史轨迹数据推导累计到达曲线。以时段网联车辆轨迹为输入,将轨迹叠加到同一周期,采用核密度估计方法拟合车辆的到达时间分布,从而生成到达率在周期内的时变系数a(t)。相应的,周期内时变到达率函数啊λ(t)可以计算为λ0a(t),其中λ0为平均到达率,为未知量。随后,基于简化的流密速基本图可以推导周期内的瞬时到达率和交通波波速的映射关系,从而可以对周期内时变交通波波速进行积分得到累计到达曲线Sa,该曲线是以λ0为自变量的函数。
然后,基于观测的排队网联车辆轨迹的离开排队关键点,采用Huber回归方法实现累计离开曲线的鲁棒回归,有效地排除异常轨迹的影响。因此,可以得到包含未知参数λ0的交叉口累计流图,进一步可以推导得到流量、排队长度、车均延误、总延误等参数与λ0之间的函数关系。
而后,鉴于网联车辆轨迹数据可以提供车辆详细的运动过程,从而可以基于轨迹数据估计交叉口的总延误,通过最小化估计的总延误与累计流图推导的总延误之间的差值,可以标定得到λ0,从而实现当前配时下的累计流图估计。
最终,可以将该框架拓展至任意候选配时下的累计流图预测。考虑累计到达曲线估计的数据驱动特性,可以通过更新候选周期下的时变系数p(t)实现候选配时下的累计流图的预测。此外,累计离开曲线可以依据候选相位红灯时长同步更新,从而实现候选配时下的累计流图预测
基于VISSIM仿真验证,不同渗透率下的由累计流图推导的流量、排队长度、总延误和平均延误估计精度如图3所示。除平均延误外,其他交通状态参数的估计精度都随着渗透率的增大而提升,特别是在渗透率小于0.15时,提升更为显著。在渗透率超过0.2后,精度提升趋于平缓。依据各渗透率的箱型图大小范围可知,在高渗透率下估计结果更为稳定。在接近现实交叉口的0.10的渗透率条件下,排队长度、总延误和流量的MAPE分别为10%、9%和9%。在0.05的低渗透率条件下,MAPE分别为17%、12%和16%。这表明本研究算法在低渗透率条件下依然可以实现较为准确的交通状态参数估计。至于平均延误,由于其是通过总延误除以流量间接计算获得,其估计误差同时受到二者误差的影响,因此其估计精度的变化呈现与其它指标不同的趋势。
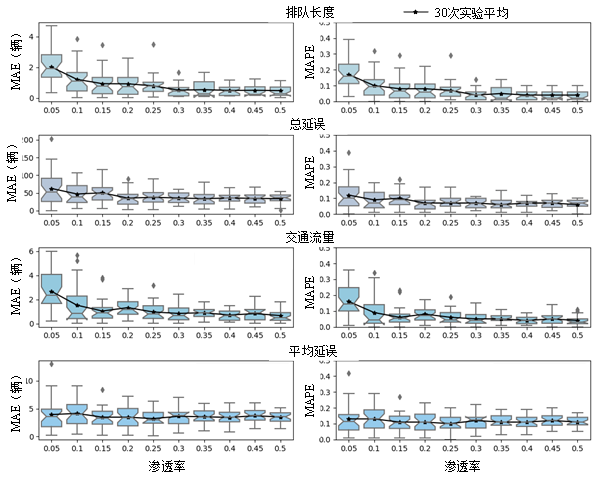
图3 不同渗透率下交通状态参数估计精度
不同候选配时下的预测结果如图4所示,其中,方案5的结果即为前述累计流图估计在0.1渗透率下的估计结果。由于各候选配时采用的到达率即为估计的到达率,因此候选配时下的流量预测误差是完全相同的。至于排队长度和总延误,可以看出各候选配时下的预测误差并无显著差异。因此,可以说明本研究提出的累计流图演化框架不仅可以准确估计当前配时下的累计流图,同样可以准确预测任意候选配时下的累计流图。

图4 候选配时下的交通状态参数预测结果
此外,该方法在深圳市福中路皇岗路进行了实证,且与现有的排队长度和流量估计方法进行对比验证,排队长度估计为MAP方法(谈超鹏, 姚佳蓉, 曹喻旻, 唐克双*. 基于网联车辆轨迹数据的周期排队长度估计[J]. 中国公路学报, 2021, 34(7): 140-151. DOI: https://doi.org/10.19721/j.cnki.1001-7372.2021.07.011),流量估计为张量方法(Keshuang Tang, Chaopeng Tan, Yumin Cao, Jiarong Yao, Jian Sun*, “A Tensor Decomposition Method for Cycle-based Traffic Volume Estimation Using Sampled Vehicle Trajectories.” Transportation Research Part C: Emerging Technologies, 2020, 118, 102739. DOI: https://doi.org/10.1016/j.trc.2020.102739)。考虑到两种模型皆为周期级估计模型,因此其最终结果采用时段内各周期估计结果的平均值。
各方法的最终估计结果如表1所示。在时段平均流量和排队长度的估计上,三种模型都表现出色。基于累计流图的流量和排队长度估计MAPE分别为2.7%和3.3%。张量模型的流量估计MAPE为4.6%,略高于基于累计流图的流量估计;MAP模型的排队长度估计MAPE仅为2.4%,略低于基于累计流图的排队长度估计。
表1 各模型交通状态估计结果
交通状态参数 |
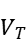 (辆/车道) (辆/车道)
|
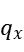 (米) (米)
|
真实值 |
21.4 |
114.7 |
累计流图 |
估计值 |
20.8 |
110.9 |
MAE |
0.6 |
3.8 |
MAPE |
2.7% |
3.3% |
MAP模型 |
估计值 |
- |
112 |
MAE |
- |
2.7 |
MAPE |
- |
2.4% |
张量模型 |
估计值 |
22.4 |
- |
MAE |
1 |
- |
MAPE |
4.6% |
- |
累计流图估计结果如图5所示。由于验证交叉口位于干道上,周期内的网联车辆轨迹到达呈现显著的车队到达模式,在红灯期间和绿灯期间各有一个车队到达。此外,可以注意到在接近排队末尾的位置网联车辆轨迹的加入排队点可能会偏离累计到达曲线。这是因为研究的模型采用固定的停车车头间距,而实际中的车辆停车车头间距存在差异,因此由车头间距造成的排队位置误差会随着排队车辆的增加而累计。尽管如此,估计的平均到达率和排队长度都与真实值几乎一致,表明累计流图的估计结果是准确可靠的。
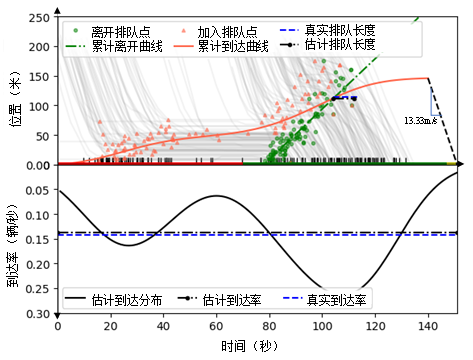
图5 实证场景下的累计流图估计结果
该研究的主要贡献在于:1)提出了一个数据驱动框架,以网联车辆轨迹数据为输入,基于累计流图描绘交叉口交通运行。其中累计到达曲线是基于轨迹数据采用非参数估计方法生成的,因此该框架无需任何车辆到达假设,适用于多种车辆到达模式。2)采用基于Huber函数的鲁棒回归方法实现累计离开曲线估计,使得该框架可以剔除异常数据的影响。3)面向当前配时的累计流图估计可以实现交叉口交通运行的全面评价,同时得到流量、排队长度、车均延误和总延误等交通参数。4)面向任意候选配时的累计流图预测使得该研究可以进一步用于信号控制优化,或无需软件仿真即可实现优化效果的快速预评估。

