作者:谈超鹏,姚佳蓉,唐克双*
已见刊于:中国公路学报, 2021, 34(11): 282.
关键词:交通工程;排队长度分布;核密度估计;车辆轨迹;停车位置分布;平均排队长度
排队长度是评价信号控制交叉口运行状态的重要参数之一。现有大多数基于抽样车辆轨迹数据的排队长度估计方法可以实现周期级排队长度估计,但是需要信号配时、渗透率或车辆到达分布等实践中难以获取的输入信息。此外,这类方法在低渗透率条件下往往难以确保估计结果的准确性和可靠性,极大地限制了其实用性。因此,本文提出了一种抽样车辆轨迹数据驱动的时段级信号控制交叉口排队长度分布估计方法,可不依赖任何交通流理论模型和前述输入信息实现排队估计。
首先,本文通过理论推导证明了时段内抽样车辆的停车位置分布和排队长度分布之间可互相转化。图1(a)展示了研究时段内个周期的排队长度,若将各周期排队长度按降序排序,则可以得到如图1(b)所示的排队长度有序序列。如果逐个位置统计排队的车辆数,即统计排队长度不小于该位置的周期数,可以得到停车位置分布,如图1(c)所示。容易证明图1(b)、(c)是关于直线y=x的轴对称图形。也就是说,如果可以获取全样本车辆的停车位置分布,那么通过这种对称关系可以进一步得到研究时段内的排队长度分布。另一方面,全样本车辆和抽样车辆的停车位置分布存在一定的相似性,如图2所示。因此,排队长度分布估计问题就转化为抽样车辆排队长度有序序列曲线的对称变换和放缩变换问题。
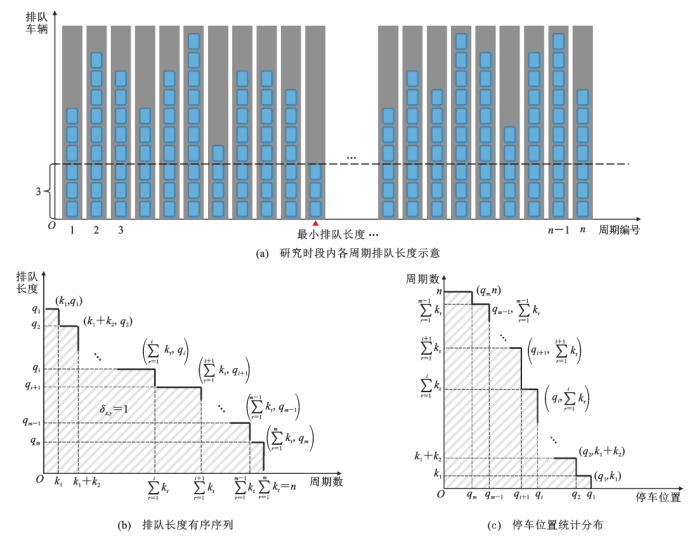
图1 排队长度有序序列与停车位置统计分布对称关系示意
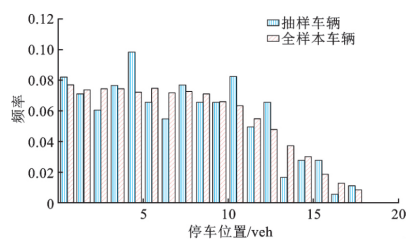
图2 抽样车辆与全样本车辆停车位置分布
其次,本文提出了一种扩展的核密度估计方法来拟合并平滑抽样车辆停车位置分布,解决了由于停车位置样本集存在下界0,而导致普通核密度估计方法在0值附近失真的问题。由于停车位置分布的横坐标与排队长度有序序列的纵坐标是相对应的,通过对停车位置分布曲线进行采样,提取其横坐标,可以得到排队长度有序序列的估计值,如图3所示。在得到排队长度有序序列后,本文采用核密度估计方法拟合最终的排队长度分布。
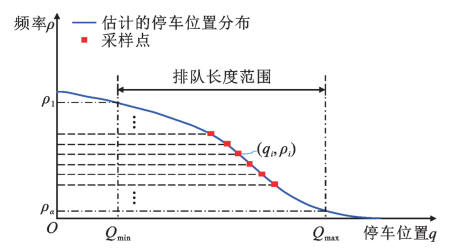
图3 抽样车辆停车位置分布曲线采样示意
最后,本文基于前述推导和拟合的停车位置分布实现了时段排队长度分布、平均排队长度和百分位排队长度估计。分别采用仿真和实证数据对上述方法进行验证和评价。结果表明,通过叠加5d相同时段的抽样轨迹数据,15min的平均排队长度估计误差仅为1.59veh,相对误差仅为9%。同时,面向不同分析时长,只要给定超过100veh抽样车辆的观测样本,无论渗透率高低,所提出的方法在定时或自适应信号控制交叉口都可实现时段排队长度分布的准确估计,其成果可进一步用于信号控制交叉口运行可靠性评估以及多时段定时信号控制的鲁棒优化。
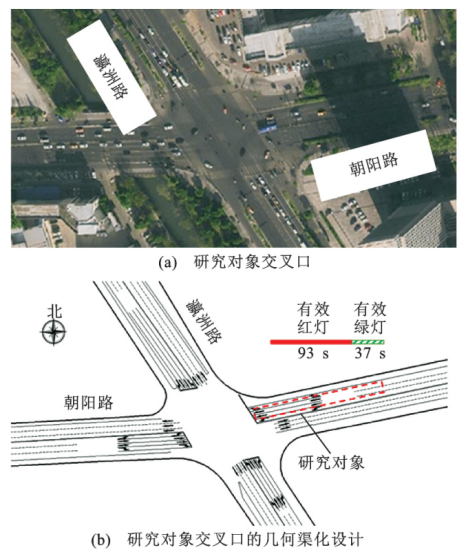
图4 仿真验证场景
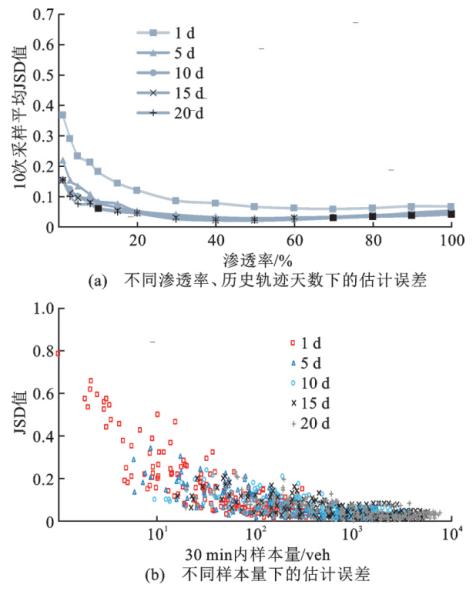
图5 仿真场景排队长度分布估计结果
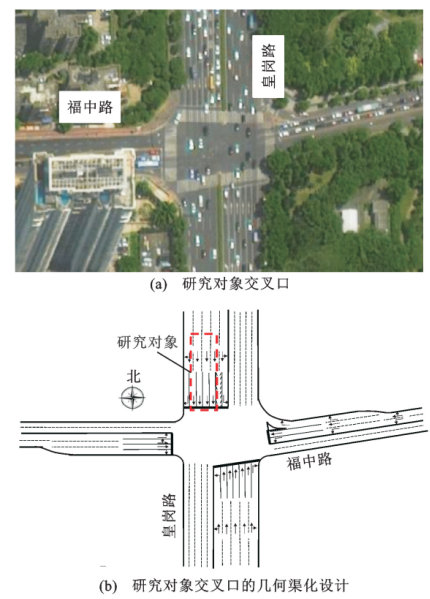
图6 实地验证场景
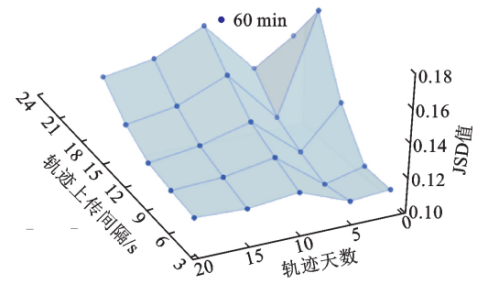
图7 实地场景排队长度分布估计结果
本文的学术贡献主要包括以下3点:①从理论上推导并解析了抽样轨迹排队位置与周期排队长度有序序列之间的内在联系,并将其运用于排队长度分布估计,作为一种数据驱动的方法丰富了排队长度估计的方法论体系。②所提排队长度分布估计方法无需任何先验交通流、信号配时或渗透率等信息,克服了大多数现有方法因需要这类信息而难以推广实际应用的缺陷。③所提方法可以应用于大规模路网,对不同到达类型、不同信号类型交叉口都适用。

