作者：谈超鹏，姚佳蓉，曹喻旻，唐克双*.

已见刊于：中国公路学报. 第34卷, 第7期, pp. 140-151. https：//doi.org/10.19721/j.cnki.1001-7372.202107.011

关键词：交通工程；排队长度估计；最大后验概率估计；网联车辆轨迹；历史轨迹数据；先验分布

排队长度是信号控制交叉口交通状态评价和优化的重要参数之一，不同检测条件下的信号控制交叉口周期最大排队长度估计一直是研究的热点和难点之一。目前，基于网联车辆轨迹数据的排队长度估计的研究可以大体分为模型驱动方法和数据驱动方法两大类，模型驱动方法包括基于交通波理论的确定性方法和基于概率统计的随机性方法，其分别通过重构周期内车辆排队的集计和消散过程和基于特定的车辆到达分布假设实现排队长度的估计，然而在极低渗透率条件（网联车辆轨迹数不超过1veh/周期）下该类方法的精度和可靠性难以保证。数据驱动方法通过对时段内的网联车辆轨迹进行集计处理，来保证排队长度的估计精度。然而，该类方法仅能得到排队长度分布、平均排队长度等时段总体特征值，无法实现排队长度的周期级估计。

现有方法尚未有效解决低渗透率条件下周期级排队长度的准确可靠估计问题。因此，本研究面向低渗透率网联车辆轨迹数据环境，提出一种融合历史和实时网联车辆轨迹数据的信号控制交叉口周期最大排队长度估计方法，并通过仿真和实证验证，对比分析了本文方法与现有同类方法的优劣，以及本文方法在不同渗透率条件下的估计精度和敏感性。

本研究的方法流程如图1所示。首先，对历史网联车辆轨迹数据（过去多天同一时段内的网联车辆轨迹数据）中蕴含的时空信息进行挖掘。空间信息层面，基于历史网联车辆的停车位置分布可以估计对应时段的排队长度分布作为先验分布。时间信息层面，基于历史网联车辆的周期内到达信息，可以得到周期内车辆的到达分布。然后，结合该到达分布与周期内实时观测的网联车辆轨迹数据，可

以构建周期排队长度的似然函数。最终，基于贝叶斯理论，可以推导排队长度的后验分布，并采用最大后验概率方法实现周期最大排队长度的估计。

图1 研究方法流程

首先，基于历史网联车辆轨迹数据的停车位置信息，可以推导得到时段内排队长度分布作为先验分布。如图2所示，对于特定时段内的全样本车辆，其停车位置频数分布与排队长度的有序序列（帕累托柱状图）存在对称关系。另一方面，考虑网联车辆在交通流中随机分布的特性，大样本条件下抽样网联车辆的停车位置频率与全样本车辆的停车位置频率服从同种分布。因此，基于抽样网联车辆的停车位置分布，可以推导得到排队长度有序序列。具体步骤包括：①采用扩展核密度估计方法对网联车辆停车位置分布进行平滑及拟合；②对网联车辆停车位置分布沿纵坐标进行均匀采样，提取采样点的横坐标，即为排队长度有序序列的估计值；③基于排队长度有序序列估计值，得出排队长度分布，作为先验分布。

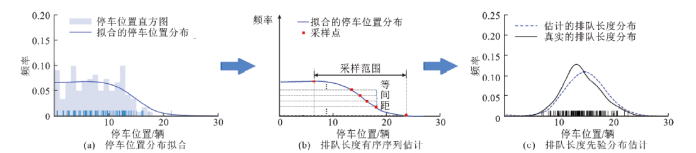
图2 排队长度先验分布估计

其次，依据周期内是否观测到排队的网联车辆，将周期分为２类场景：观测到排队网联车辆的周期和未观测到排队网联车辆的周

期。如图3所示，对于观测到排队网联车辆的周期，依据周期内最后１辆排队网联车辆的映射到达时刻及排队位置，推导得到排队长度的似然函数，该似然函数中，到达率作为中间变量，不包含在最终的推导结果中。对于未观测到排队的网联车辆的周期，认为其观测到的最后１辆排队网联车辆的位置为０。因此，面向２种类型的周期，本研究似然函数中均无需到达率参数。近一步，依据周期内观测的最后１辆排队的网联车辆和第１辆非排队的网联车辆的轨迹，可以确定可能的排队长度的取值范围。

图3 排队长度似然函数推导示意

最后，为了克服低渗透环境下观测信息不足的缺陷，本研究在参数估计中加入经验信息，即参数的先验分布，以提升参数的估计精度。本研究中，基于历史网联车辆轨迹已得到排队长度先验分布和基于周期实时观测的网联车轨迹可以推导排队长度似然函数，依据贝叶斯理论，可以近一步推导排队长度的后验分布，从而采用最大后验概率估计算法，实现周期级排队长度的估计。

本研究分别在仿真场景和实证场景下对所提出方法进行了效果验证。其中，仿真案例以江苏省连云港市朝阳路３个连续交叉口为背景建立微观仿真模型，由电警和地磁采集的流量、转向比、大车比例等数据对模型进行标定， 选取同类型的极大似然估计方法（MLE）进行效果对比，并分别设置饱和度为0.48和0.83两个低渗透轨迹场景以进一步测试方法在不同流量水平下的精度。不同渗透率下本文提出的MAP方法与对比的MLE方法的精度如图4所示。

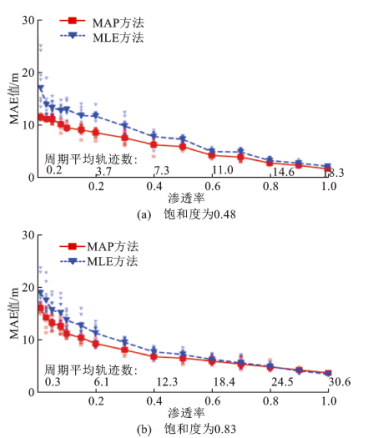
图4 不同饱和度和渗透率下２种方法估计误差结果对比

由图4可见：即便在低渗透环境下，本方法在２个饱和度场景下的MAE值分别仅为12ｍ（不超过２辆车）和16ｍ（不超过３辆车）。当周期平均轨迹数超过３条时，平均MAE在２个饱和度场景下都下降到个位数。此外，与MLE方法相比，本文提出的MAP方法在各渗透率下都表现出更高的估计精度，且在低渗透率下估计精度的优势更为显著。10次不同随机样本的平行试验的散点结果显示，MAP方法的散点分布也比MLE方法更为集中，展现出更好的稳定性。同时，相比之下，MAP方法无需估计到达率，其在融合排队长度的先验信息后，可以有效地克服周期内轨迹信息不足的问题。

图5展现了在２个常见渗透率水平下MAP方法和MLE方法的周期级估计排队长度的估计结果，渗透率3％（0.03）对应中小城市常面临的低渗透轨迹环境，渗透率10％（0.1）对应大城市主干路口的渗透率水平。由图5可见，在低渗透轨迹环境下，大量的周期未观测到网联车辆轨迹，因此可能的排队长度范围也较大。MLE方法估计值整体偏离真实排队长度，呈现明显的过估计；相比之下，由于考虑了先验分布，MAP方法可以产生更接近平均排队长度的估计值。在渗透率为0.1的条件下，几乎所有周期都可以观测到网联车辆，排队长度的取值区间也较为集中，MLE方法和MAP方法的估计结果更贴合真实排队长度的波动，但MAP方法估计值更接近平均排队长度，偏差更小，精度更高。

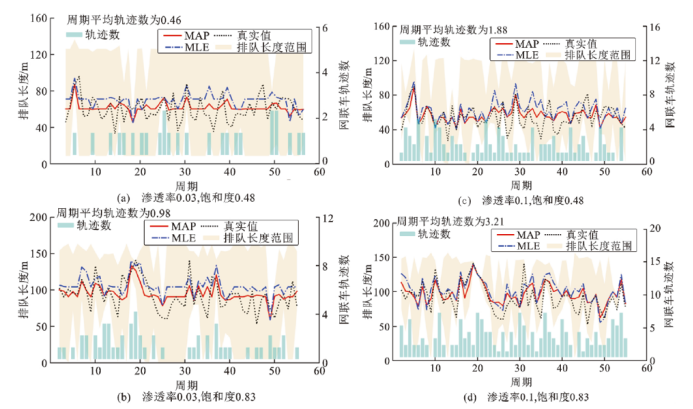
图5 两个常见渗透率下周期排队长度估计结果

实证场景验证地点为深圳市福中路—皇岗路交叉口，研究对象为北进口道４条直行车道，如图6(a)、(b)所示。网联车辆轨迹数据采集时间为2017年4月13日9:30～14:30，轨迹上传频率为3s。真实的交通状态由高清摄像机记录，并通过人工计数的方式提取了各周期的通过流量，如图6(c)所示。其中，２个不同流量水平的时段被选取做验证，时段１为10:10~11:40，包含31个周期；时段2为11:40~12:40，包含25个周期。平均渗透率分别为8.96％和8.49％。该交叉口采用SMOOTH自适应控制系统控制，信号配时参数随实际流量波动。

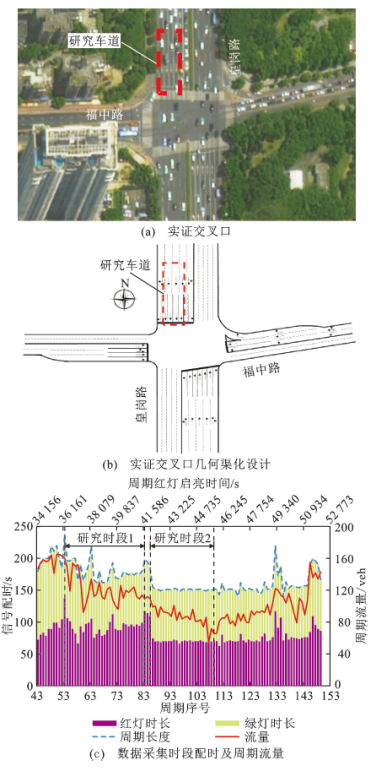
图6 实证交叉口

两个研究时段的先验分布与最大排队长度估计结果如图7所示。由图7可见：估计的先验分布可以较为准确地反映真实排队的分布情况，且估计分布均值与真实分布均值的误差在１辆车以内。在实

证场景中，大多数周期内MAP方法和MLE方法的估计结果都相同。这是因为２个研究时段内周期平均网联车辆轨迹数分别为10.7条和7.2条，各周期的排队长度取值范围十分有限，周期内充足的轨迹提供的信息使得MLE方法本身就能达到较高的精度，所以考虑排队长度先验分布的MAP方法对精度的提升有限。但是，对于MLE产生过大或过小的估计值的周期（如周期69~72），在排队长度上下界允许的范围内，MAP方法仍然可以产生更为准确的估计结果。注意到，部分周期出现真实排队长度在可能的排队长度范围之外的情况。这是因为排队长度范围是通过网联轨迹确定的，轨迹生成的排队长度单位为ｍ，而真实的排队长度是通过视频人工计数得到，其单位为veh，在进行度量转换的过程中存在一定误差。

图7 两个研究时段的周期排队长度估计结果

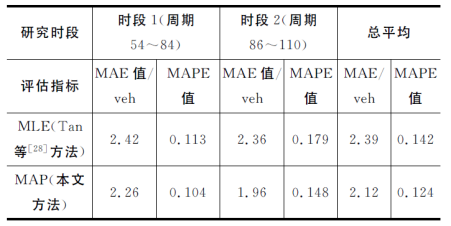
实证场景的平均结果如表１所示。由表１可知：总体上，在２个研究时段内，MAP方法的估计误差均小于MLE方法。MAP方法在两个时段的平均误差分别为2.26辆和1.96辆，平均相对百分误差分别为10.4％和14.8％，均优于现有的MLE方法。此外，时段１信号配时波动较大，时段２则较为稳定。在两个时段下的先验分布估计与最大排队长度估计精度并无显著差异，因此本文的方法对周期长度不敏感。

表 1 实证结果对比

本研究的主要学术贡献在于：①挖掘历史网联车辆轨迹数据，基于贝叶斯理论将排队长度的先验分布应用于周期排队长度估计中，提高排队长度的估计精度和稳定性；②不同于现有方法，无需预设车辆到达率等交通参数即可估计不同轨迹数据条件下的周期排队长度，解决了低渗透率条件下排队长度估计精度难以保障的问题，且同时适用于网联车辆渗透率较高和较低的信号控制交叉口。